Recently, a proof of the collatz conjecture was presented. While the proof seems convincing, it does contain a critical flaw.

Background

The core of the proof’s argument is that the lowest order bits will be turned into zeros faster than new ones can be added to the high order bits. While that is true in most cases, it may not be true in all cases.

Counterargument

The main problem with the proof presented is that the low order bit does not always move as many places as the proof claims, allowing for the possibility that a number could contain a bit pattern that will cause the low order bits to continually trail behind the high order bits, preventing the recurrence from ever reaching one.

Definitions

In this argument it will be necessary to refer to individual bits within a binary number. Two bits of particular interest are the hob (highest order bit) and the lob (lowest order bit) which are the highest and lowest order non-zero bits, respectively. To refer to other bits, the functions hob(x, y) and lob(x, y) return zero or one based on the specified bit relative the highest and lowest order non-zero bits, wheres y indicates the relative position offset from the appropriate end. If the second parameter is omitted, y is assumed to be zero.

Decision Trees

By applying 3x+1 to all of the odd numbers from 2¹⁸+1 to 2²¹-1, it’s possible to enumerate all of the possible changes in hob and lob positions after the next iteration. Decision trees to predict those changes based on bits in the current number can then be built from that data.

Below is a tree where the leaves give the number of places that the highest order bit will have moved after a the next application of 3x+1. As expected, after a single iteration the high order bit can move either 1 or 2 bits.

Decision tree to predict the change in highest order bit position after one iteration.

Similarly, a decision tree can be built to predict the movement of the low order bits. The tree below shows the number of places that the lowest order bit place moves.

Decision tree to predict the change in lowest order bit position after one iteration.

While the high order bit change shows the hob can only move by up to two bits per application of 3x+1, the lob can move many more places. This is exactly what would be expected based on the claims in the original proof. However, there are also cases where the lob can move by only one bit while the hob moves by two.

If these trees are extended to predict the change after two iterations, the problem becomes more pronounced. Below are two trees that predict the number of places that the hob and lob will move after two iterations.

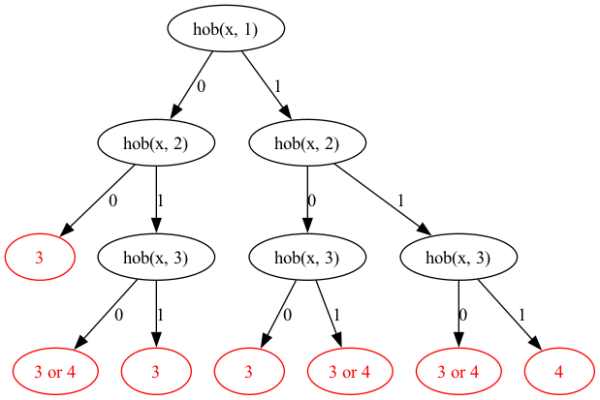
Decision tree to predict the change in highest order bit position after two iterations.

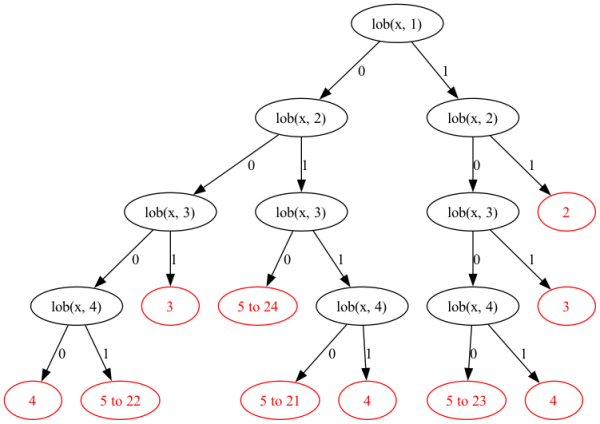
Decision tree to predict the change in lowest order bit position after two iterations.

In the above trees, it is clear that after two applications of the 3x+1 rule, the high order bits will move either 3 or 4 bits, while the low order bit will move by 2 to 24 positions (limited due to the sample size used).

These two iteration trees more clearly show that while the high order bit will move up to 4 positions after two iterations, the low order bit might only move 2 or 3, which means there are cases where the gap between the hob and the lob will increase.

This makes it difficult to eliminate the possibility that there may exist numbers such that their internal bits will cause the low order bits to not be consumed as quickly as new high order bits are added, allowing for sequences of numbers that gain bits indefinitely and racing off towards infinity instead of reaching one.

It may be possible to use these patterns to construct a number that will diverge, however that is a question for another time.

Conclusion

Using decision trees, it can be shown that there is a possible mechanism for the collatz recurrence to cause the gap between the highest and lowest order non-zero bits to increase indefinitely, allowing for the possibility that there may be a number that can cause the low order bits to move up more slowly than the high order bits, causing the value to grow forever.